Earley parser
In computer science, the Earley parser is an algorithm for parsing strings that belong to a given context-free language, named after its inventor, Jay Earley. The algorithm is a chart parser that uses dynamic programming, and is mainly used for parsing in computational linguistics.
Earley parsers are appealing because they can parse all context-free languages, unlike LR parsers and LL parsers which are more typically used in compilers but which can only handle restricted classes of languages. The Earley parser executes in cubic time in the general case 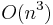 , where n is the length of the parsed string, quadratic time for unambiguous grammars
, where n is the length of the parsed string, quadratic time for unambiguous grammars 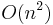 , and linear time for almost all LR(k) grammars. It performs particularly well when the rules are written left-recursively.
, and linear time for almost all LR(k) grammars. It performs particularly well when the rules are written left-recursively.
Contents |
The algorithm
In the following descriptions, α, β, and γ represent any string of terminals/nonterminals (including the empty string), X and Y represent single nonterminals, and a represents a terminal symbol.
Earley's algorithm is a top-down dynamic programming algorithm. In the following, we use Earley's dot notation: given a production X → αβ, the notation X → α • β represents a condition in which α has already been parsed and β is expected.
For every input position (which represents a position between tokens), the parser generates an ordered state set. Each state is a tuple (X → α • β, i), consisting of
- the production currently being matched (X → α β)
- our current position in that production (represented by the dot)
- the position i in the input at which the matching of this production began: the origin position
(Earley's original algorithm included a look-ahead in the state; later research showed this to have little practical effect on the parsing efficiency, and it has subsequently been dropped from most implementations.)
The state set at input position k is called S(k). The parser is seeded with S(0) consisting of only the top-level rule. The parser then iteratively operates in three stages: prediction, scanning, and completion.
- Prediction: For every state in S(k) of the form (X → α • Y β, j) (where j is the origin position as above), add (Y → • γ, k) to S(k) for every production in the grammar with Y on the left-hand side (Y → γ).
- Scanning: If a is the next symbol in the input stream, for every state in S(k) of the form (X → α • a β, j), add (X → α a • β, j) to S(k+1).
- Completion: For every state in S(k) of the form (X → γ •, j), find states in S(j) of the form (Y → α • X β, i) and add (Y → α X • β, i) to S(k).
These steps are repeated until no more states can be added to the set. The set is generally implemented as a queue of states to process (though a given state must appear in one place only), and performing the corresponding operation depending on what kind of state it is.
Pseudocode
Adapted from Speech and Language Processing by Daniel Jurafsky and James H. Martin
function EARLEY-PARSE(words, grammar) ENQUEUE((γ → •S, 0), chart[0]) for i ← from 0 to LENGTH(words) do for each state in chart[i] do if INCOMPLETE?(state) then if NEXT-CAT(state) is a nonterminal then PREDICTOR(state, i, grammar) // non-terminal else do SCANNER(state, i) // terminal else do COMPLETER(state, i) end end return chart procedure PREDICTOR((A → α•B, i), j, grammar), for each (B → γ) in GRAMMAR-RULES-FOR(B, grammar) do ADD-TO-SET((B → •γ, j), chart[ j]) end procedure SCANNER((A → α•B, i), j), if B ⊂ PARTS-OF-SPEECH(word[j]) then ADD-TO-SET((B → word[j], i), chart[j + 1]) end procedure COMPLETER((B → γ•, j), k), for each (A → α•Bβ, i) in chart[j] do ADD-TO-SET((A → αB•β, i), chart[k]) end
Example
Consider the following simple grammar for arithmetic expressions:
<P> ::= S # the start rule <S> ::= <S> "+" <M>|<M> <M> ::= <M> "*" <T>|<T> <T> ::= "1" | "2" | "3" | "4"
With the input:
2 + 3 * 4
This is the sequence of state sets:
(state no.) Production (Origin) # Comment ----------------------------------------- == S(0): • 2 + 3 * 4 == (1) P → • S (0) # start rule (2) S → • S + M (0) # predict from (1) (3) S → • M (0) # predict from (1) (4) M → • M * T (0) # predict from (3) (5) M → • T (0) # predict from (3) (6) T → • number (0) # predict from (5) == S(1): 2 • + 3 * 4 == (1) T → number • (0) # scan from S(0)(6) (2) M → T • (0) # complete from (1) and S(0)(5) (3) M → M • * T (0) # complete from (2) and S(0)(4) (4) S → M • (0) # complete from (2) and S(0)(3) (5) S → S • + M (0) # complete from (4) and S(0)(2) (6) P → S • (0) # complete from (4) and S(0)(1) == S(2): 2 + • 3 * 4 == (1) S → S + • M (0) # scan from S(1)(5) (2) M → • M * T (2) # predict from (1) (3) M → • T (2) # predict from (1) (4) T → • number (2) # predict from (3) == S(3): 2 + 3 • * 4 == (1) T → number • (2) # scan from S(2)(4) (2) M → T • (2) # complete from (1) and S(2)(3) (3) M → M • * T (2) # complete from (2) and S(2)(2) (4) S → S + M • (0) # complete from (2) and S(2)(1) (5) S → S • + M (0) # complete from (4) and S(0)(2) (6) P → S • (0) # complete from (4) and S(0)(1) == S(4): 2 + 3 * • 4 == (1) M → M * • T (2) # scan from S(3)(3) (2) T → • number (4) # predict from (1) == S(5): 2 + 3 * 4 • == (1) T → number • (4) # scan from S(4)(2) (2) M → M * T • (2) # complete from (1) and S(4)(1) (3) M → M • * T (2) # complete from (2) and S(2)(2) (4) S → S + M • (0) # complete from (2) and S(2)(1) (5) S → S • + M (0) # complete from (4) and S(0)(2) (6) P → S • (0) # complete from (4) and S(0)(1)
The state (P → S •, 0) represents a completed parse. This state also appears in S(3) and S(1), which are complete sentences.
See also
References
- Aycock, John; Horspool, R. Nigel (2002), "Practical Earley Parsing", The Computer Journal 45 (6): 620–630, doi:10.1093/comjnl/45.6.620.
- Earley, Jay (1970), "An efficient context-free parsing algorithm", Communications of the ACM 13 (2): 94–102, doi:10.1145/362007.362035.
- Leo, Joop M. I. M. (1991), "A general context-free parsing algorithm running in linear time on every LR(k) grammar without using lookahead", Theoretical Computer Science 82 (1): 165–176, doi:10.1016/0304-3975(91)90180-A, MR1112117.
- Tomita, Masaru (1984). "LR parsers for natural languages". COLING. 10th International Conference on Computational Linguistics. pp. 354–357.
External links
C Implementations
- 'early' An Earley parser C -library.
- 'C Earley Parser' An Earley parser C.
Java Implementations
- PEN A Java library that implements the Earley algorithm.
- Pep A Java library that implements the Earley algorithm and provides charts and parse trees as parsing artifacts.
- [1] A Java implementation of Earley parser.
Perl Implementations
- Marpa::XS and Marpa::PP, Perl modules, incorporating improvements made to the Earley algorithm by Joop Leo, and by Aycock and Horspool.
- Parse::Earley An Perl module that implements Jay Earley's original algorithm.
Python Implementations
- Charty a Python implementation of an Earley parser.
- NLTK a Python toolkit that has an Earley parser.
- Spark an Object Oriented "little language framework" for Python that implements an Earley parser.
- earley3.py A stand-alone implementation of the algorithm in less than 150 lines of code, including generation of the parsing-forest and samples.
Common Lisp Implementations
- CL-EARLEY-PARSER A Common Lisp library that implements an Earley parser.
Scheme/Racket Implementations
- Charty-Racket A Scheme / Racket implementation of an Earley parser.